Have Fun Staying Warm
|
A completely new way to heat your house ! Just imagine an expensive hair dryer that just happens to make money ! Bitcoin mining hardware - ASIC's - blow out lots of warm air, why not use it to heat your house? Power it with 100% renewable electricity and you have zero emissions heating ! Once set up it's just a matter of flicking a switch or setting a timer to turn it on, then eventually selling or (much better hodling) the resulting Bitcoin to pay for the electricity.
Ditching gas & going all electric saves money in quite a few different ways -
Also don't forget to factor in buying an ASIC every 2-4 years (£500-1400), I wouldn't buy new unless running all year. |
Fully installed Bitcoin Mine Heating
|
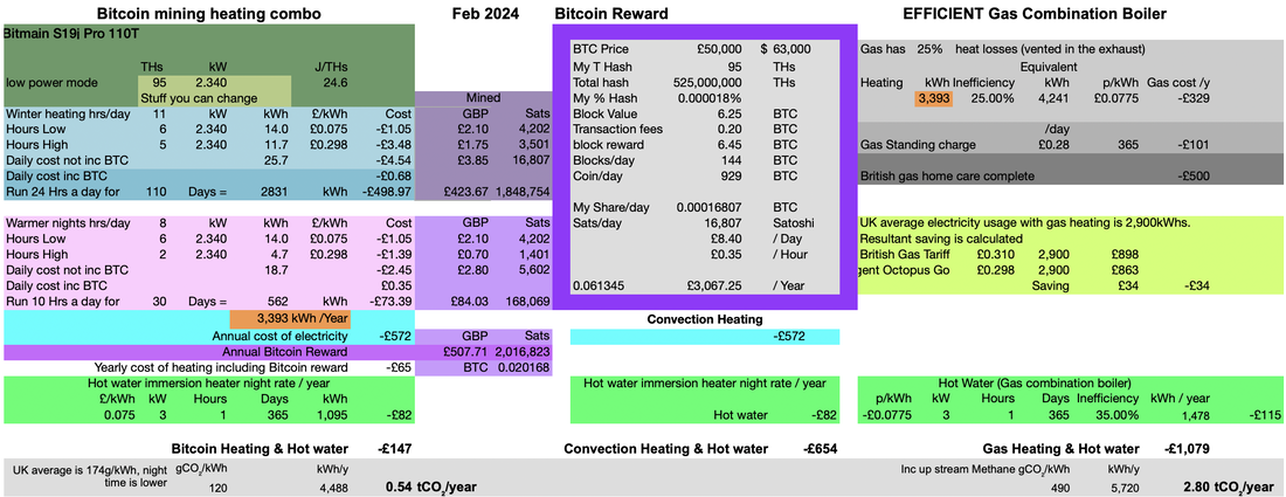
Heat for Heat comparison Bitcoin mining heating vs Gas
Bigger – less well insulated houses may need lots more heat.
This British Gas article says the average 3 bed house uses 12,000 kWh of gas (=5.9 tonne CO₂) and 2,900kWh of electricity (=0.5 tonne CO₂).
If you are the person using this much gas YOU are the person boiling the planet ! Not the bitcoin miners.
Get insulated + Heat Ventilation Recovery ASAP & stop burning fossil fuels !
This British Gas article says the average 3 bed house uses 12,000 kWh of gas (=5.9 tonne CO₂) and 2,900kWh of electricity (=0.5 tonne CO₂).
If you are the person using this much gas YOU are the person boiling the planet ! Not the bitcoin miners.
Get insulated + Heat Ventilation Recovery ASAP & stop burning fossil fuels !
BITMAIN ASIC
|
|
Bitmain S19 pro 110TH vs gas heating
Bitcoin mining heating + Battery
|
Above is my current setup with the addition of a house battery gives access to day time heat at night time prices !
Good house insulation & high thermal mass help to absorb the heat then slowly release are very helpful. My electricity from Octopus is about as cheap as you will find during off peek in the UK its for Electric Vehicle drivers only (GO / Intelligent tariff), also the addition of Octoplus & Agile tariffs introduce the possibility of free electricity or even paid to consume electricity for when the grid has a surplus. Prices change due to UK Government price cap . |
|
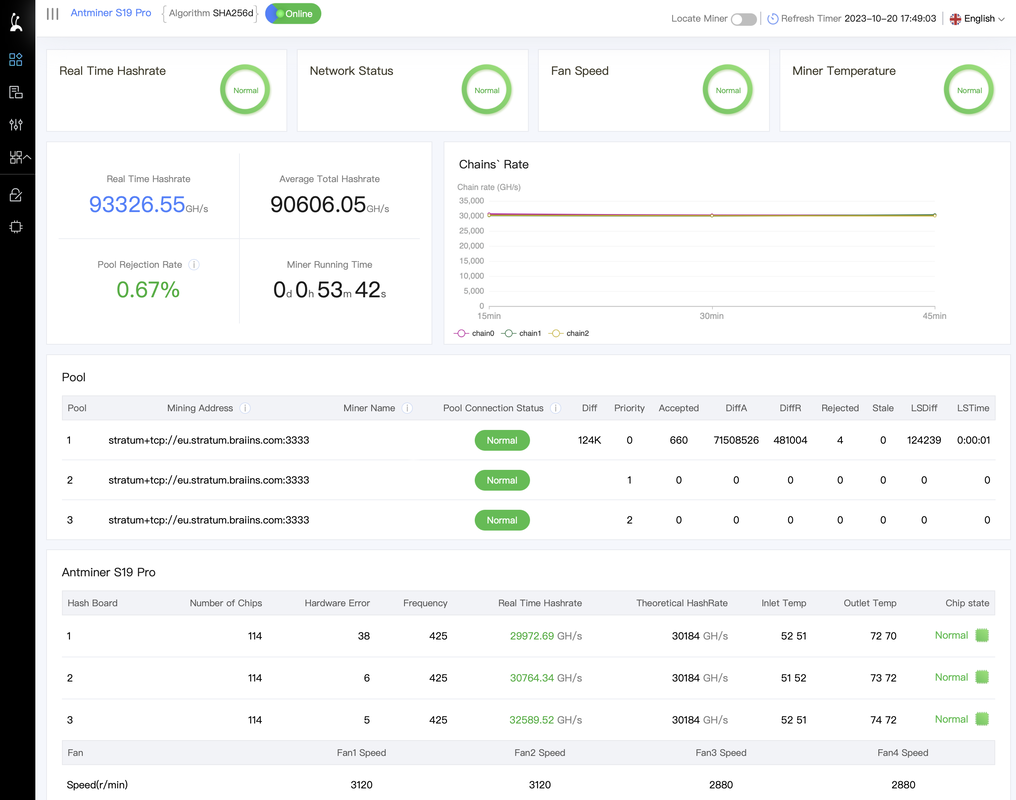
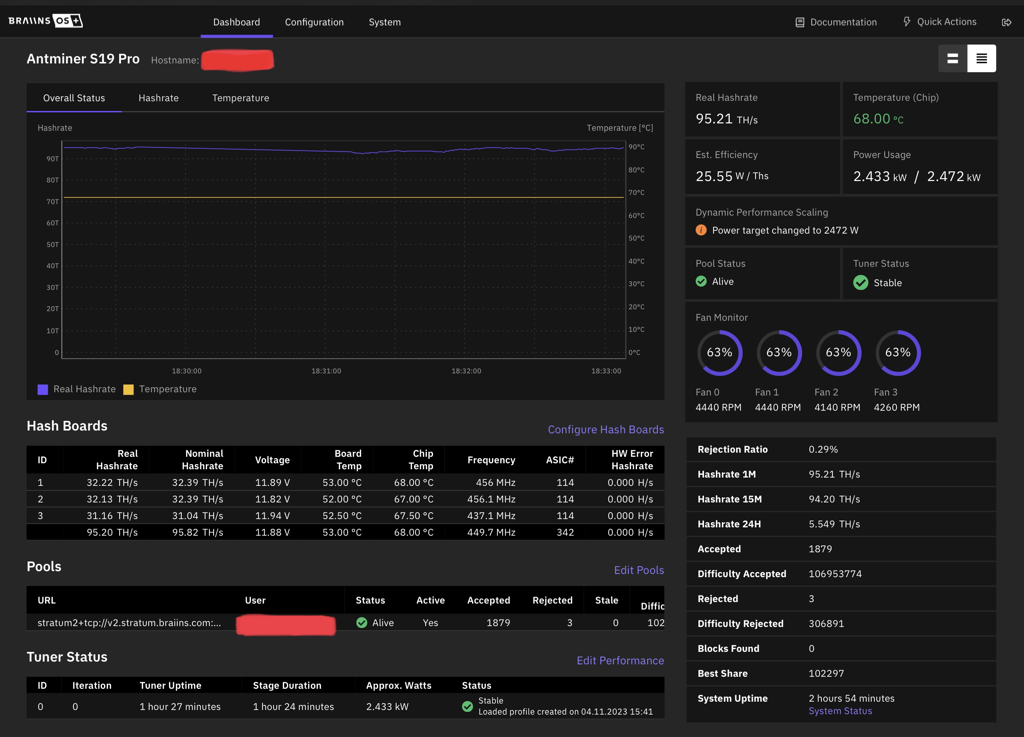
By updating the Bitmain S19 110TH software, I have now gained Low Power mode (which previously didn't exist). 90.5TH for about 2,352kW ≈ 26J/TH. My sound proof box was built to house a much smaller Bitmain T15 & struggles to cool the S19 on full power with the fans noisily hammering away at 5400 RPM. This now seem much happier on low power mode with the fans purring away at 2880 RMP occasionally going up to 4500 RPM.
Braiins software With Bitmain software I found the S19 pro fan speed keeps yo-yo ing from 2800-6180 rpm. So I thought I’d give Braiins software a try.
Initially the mine went to full power 115TH fans going max speed 5800-6200 rpm. Chip temperatures were very low 60c, so I changed the target TH to minimum the software would let me 95.858 TH & wattage to min 2472w but the fans were still trying to keep chip temps to 60c. I found changing the target temperature to 68c allowed the fans to relax to a much quieter 62% /4000rpm and 71c 53% / 3600rpm No yo-yo ing 👍 |
|
Requirements
An S9 although popular may now take 3-4 winters to reach the minimum payout (typically 0.01 BTC) . Ocean mining can now pay out via Lightning which enables much smaller but more frequent payouts. Where to buy ASICs |
Fastest Most Efficient Bitcoin Miners (December 2023)Bitmain Antminer (not including 3phase)
S2 Pro 234TH 15 J/TH 3510W S21 200TH 17.5 J/TH 3500W S19 XP 140TH 21.5 J/TH 3010W S19 110TH 29 J/TH 3100W S17 56TH 36.7 J/TH 1718W - (low power mode) S15 28TH 50 J/TH 1596W S9se 17TH 80 J/TH 1360W - Maintained popularity for a a lot longer than profitability in the US because it would run on 110V with the correct PSU, but very old hat. Avalon Miners
A1566 18.5 J/TH 185TH 3420W A1466 19.5 J/TH 170TH 3315W A1366 25 J/TH 130TH 3250W MicroBT Whatsminer M60 20 J/TH 172TH M50++ 22 J/TH MS50+ 24 J/TH 130THs 3120W |
|
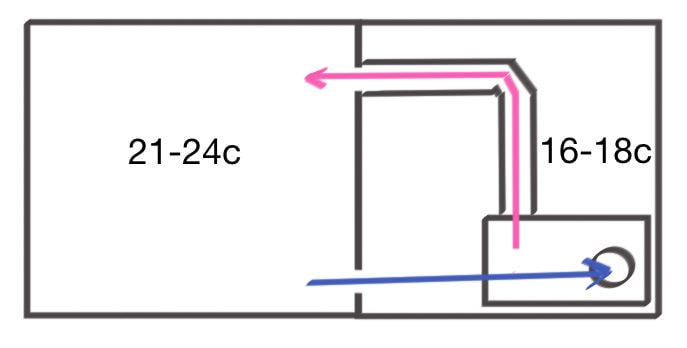
ASICs are very loud (70-90db) so they need ideally to be in a sound proof box. Venting the warm air into an adjacent room/rooms is the best way to circulate it around the property. There is such a large air flow that you may need to cut 2 holes in the adjoining walls (one in and one out) or make sure doors are propped open. I found the S17 on low power mode 47THs / 1718Watts kept the whole house warm enough down to -5c. The house is well insulated for an old house. You could experiment with a regular heater to see what wattage you need. Leave it on 48hr to see how warm the house gets you may find 3.1kW of the Bitmain S19j too much heat low power mode will reduce to about 2400w. Unfortunately some ASICs cant be turned down using standard software, but can with Braiins aftermarket software, or be switched off.
When it's too warm to mine 24 hours, I like to operate 23:30 to 05:30 taking advantage of cheap night time rate electricity. |
Room Air Flow
|
1 Year service + filter change
|
This is 1 "season" (winter months) of mining. If there were no filter, half of this dust would be stuck in the electronics & fans of the mine its self and could cause over heating, which is what I think caused my first mine to fail. It works brilliantly with no hair or dust in the mine after a year.
|
|
Bitcoin mine in a sound proof box
|
This method reduces the noise level of 1 mine down to 50 Db @ 1M. It cuts out all the high frequencies leaving you with a low rumble, like a tumble drier which can only just be heard in the next room.
These things REALY need to breathe, so reducing the air flow must be kept to an absolute minimum. The air intake best placed on the side or bottom where the air is coolest. The in and outlets need to be about 8.75" -10.75" Diameter this allows the duct to sit slightly in the hole without squashing, no fixing required. A noise reducing duct could be placed on the inlet as well & will reduce noise by a fairly unnoticeable 1 or 2Db. Vent Sizes Cross Sectional Area (CSA) The largest Vent on the T15 measures 7" x 4.5" = 31.5" Power supply vent = 2" x 1.5" = 3" Total CSA = 34.5" I recommend 10” now as all mordern ASICs are now >3kW. Even if you mine with an S9 sooner or later you will have to upgrade. So all paths through the enclosure must not be <= 34.5" CSA and preferably much bigger. Duct CSA = Area of a circle A = π r ²
10" =3.14 x 5² = 78.54" S19, S21 etc 8" = 3.14 x 4² = 50.26" OK for short runs, S9 ST15s 6" = 3.14 x 3² = 28.27" is less than the CSA of the mine therefore will restrict air flow and kill your mine. Materials Required-
Tools Required-
Box overall dimensions L = 970mm, H = 520mm, W = 582mm Wall thickness 45mm (2 x 22mm + sealant. I originally designed this box for the T15 but the latest miners S19 / S21 are bigger (400*195*290), fortunately it still fits into this size box but I had to do away with the internal partitions and widen the vents. It's ok in low power mode but if high power I'd widen the vents to 10" (250mm) or 2x 8". Noise wise the new layout doesn't seem to make a huge difference. The partition should be so the mine is in the cold air side, with top, bottom & sides exposed to cold air. the Lego here is to hold the second layer of insulation away from the surface.
Decide where your duct entry and exit are going to be so you can work out where the inner box vents will be. The air intake should be at the bottom so as to suck in cooler air from low down. Inner partitions are not glued just held in place by the second layer of insulation.
I drilled a hole for the mains and ethernet leads so it sit nicely between the vertical horizontal insulation. Saw a slot from the top to the hole, this provides a versatile cable entry & saves taking the plugs on and off.
The main box is double thickness screwed and glued with the AC50. The lid just rests on the draft excluder and is held in place with latches.
|
Air intake moved from the top to the side so its sucking the coolest air from lowest point. Seems happier!
A insulation lid is placed over this centre section, then the whole thing has one final layer of insulation. Generally 2 layers of insulation where ever possible. Be careful not to insulate the mine, don't want it getting too hot.
Draft excluder is to the top edge before placing the lid on. 
|
Running the ASIC for the first time.
A cool - well ventilated mine is a happy mine. The fans have to work slightly harder in a box, self adjusting to 2700-4500 RPM as opposed to running slower when free standing. Chip temperatures are less than 80c. Is this good or not I don't know as Bitmain do not specify a max temperature, but that is the temperature I like to stay below. The fans will increase if its to hot.
|
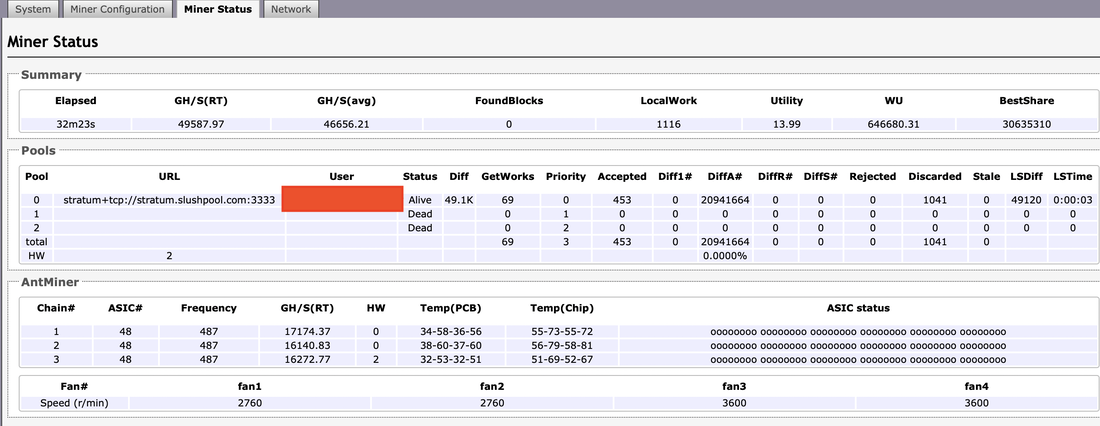
Bitmain S17 web portal
|
Run your mine free standing ( If you can bear the noise 🤪) in a cool area for a couple of hours. They can take a while to start mining especially the first time on your pool or if they been stood along time. All the fans should start immediately.
- Set up the mining pool details straight away (otherwise you'll be mining for the previous owner). Access your mine via a web browser every device has an its own I.P. address typically 192.168.1.??? . Logging into your Internet hub (hub address/password is on the router) and look at the devices that are connected. This will tell you the address.
- User name - root (Defalt)
Password - root (change this)
Point it too your mining pool. - Make sure it is hashing (if it's not hashing you don't get heat, just fan noise)
- Take a screen shot of the chip temperatures so you have a base line guide.
- Enclose the mine in your box and watch the web interface to see how its handling the air flow constraints. Over 5000 RPM & you may need to rethink the air flow situation.
Asthma It also has the added benefit of continuously cleaning the air. I have a mild dust allergy that occasionally causes asthma symptoms, this seems to have gone away since using this heating method. Also may be due to swapping the gas hob for an induction hob in my effort to decarbonise. Gas hobs are notorious causing breathing difficulties.
|
|
Bitcoin mine wiring UK
Bitcoin mining ASICs seem to be increasing in Wattage, the S17 drew about 2600W or 11.3A (2600W/230V) on full power which is just about ok for regular UK sockets that are fused at 13A Max, but now some mines can operate at 3500W or 15.2A. Too much for 1 UK socket. You could just run off 2 sockets and just manually switch both switches at the same time. If you want it on a timed circuit to take advantage of cheeper rate electricity, you need a timer. the one shown is rated at 16A so just within tolerance particularly if running in low power mode, roughly 2240W (9.7 A). Consult an electrician.
|
|
Home Mining and the Network
|
Home mining is good for the Bitcoin network in several ways -
|
|
Bitcoin mine in a fridge.
|
One years mine heating study 2020-21 Used purely as a heater during the winter 4 month period only.
Bitmain S15 28TH 1450W Cost £1300 BTC Generated = 0.07 Sold @ $10,000 or £7700 £7700 x 0.07 = £540 Cost of Electricity £580 1 year heating cost £40 |
|
Pre made home miners Some companies are starting to make free standing heaters that actually mine bitcoin.
At 40-50 Watts/THash these Heatbit room heaters are only 1/3 as efficient as the latest Bitmain S21 - 16 W/THs. Home mining innovation from futurebit Micro miners nerdminers.com |
|
Further Resources
How to repair your mine
Bimain S9 Board-Repair-Guide
Mining gude bitcoinexchangeguide.com/bitcoin-mining/
Bitcoin Magazine Home Mining , Mining for the streets
A good article on Noise Cancling
Mining gude bitcoinexchangeguide.com/bitcoin-mining/
Bitcoin Magazine Home Mining , Mining for the streets
A good article on Noise Cancling
Interesting, in-depth articles from
https://minerdaily.com/
@DailyMiner
Hashing2heating
An interesting startup utilising the heat from bitcoin mining to heat properties !
https://minerdaily.com/
@DailyMiner
Hashing2heating
An interesting startup utilising the heat from bitcoin mining to heat properties !
